qat.qpus.NoisySPD

class qat.qpus.NoisySPD(hardware_model=None, threshold: float = 1e-15, max_weight: int = None, max_size: int = None, max_x_weight: int = None, nprocs: int = 1, extract_clifford: bool = True, tol_spam_reconstruction: float = 1e-10, verbose: bool = False, disable_resource_management: bool = False, **kwargs)

Sparse Pauli Dynamics simulator QPU for noisy quantum circuits.

Four truncation modes exist, and any combination of them can be applied:

  • Threshold: Set a threshold of acceptance for the coefficients of Pauli rows. Only Pauli rows above this threshold will be tracked.

  • Max weight: Set a maximum Hamming weight. Only Pauli rows with weight below this maximum will be kept.

  • Max size: Set a maximum number of Pauli rows. If exceeded, rows with the lowest coefficients will be discarded first.

  • Max X/Y support: Set a maximum number of X or Y terms allowed in each Pauli row.

Note

If none of the truncation methods (threshold, max_weight, max_size, or max_x_weight) are set, no truncation is performed and the simulation will be exact. This is generally much less efficient than using linear algebra-based methods.

Parameters:

  • hardware_model (qat.hardware.HardwareModel, optional) – Description of the HardwareModel

  • threshold (float, optional) – Threshold of acceptance for the coefficients of the Pauli rows.

  • max_weight (int, optional) – Maximum allowed Hamming weight of the Pauli rows.

  • max_size (int, optional) – Maximum allowed size of the PauliTableau throughout the simulation.

  • max_x_weight (int, optional) – Maximum allowed number of X and Y terms in the Pauli rows.

  • nprocs (int, optional) – Number of processors to use. Defaults to 1.

  • extract_clifford (bool, optional) – If True, performs Clifford recompilation. Defaults to True.

Mathematical description

This simulator computes expectation values of observables by studying their evolution of in the Pauli basis, going through a noisy quantum circuit in reverse, applying quantum channels in reversed order. This is equivalent to studying the time evolution of a system in the Heisenberg picture rather than in the Schrödinger picture.

This simulator aims to compute the expectation value of an observable, written as:

\[<\mathcal{O}> = \mathrm{Tr}[ \rho_0 U^{\dagger} \mathcal{O} U ]\]

where \(\rho_0 = \ket{0 ... 0} \bra{0 ... 0}\), \(<\mathcal{O}>\) is an observable and \(U\) is a noisy quantum circuit composed of quantum channels.

\[U = \mathcal{E}_L \circ ... \circ \mathcal{E}_1\]

The quantum channels are expressed using the chi-matrix formalism, as

\[\mathcal{E}(\rho) = \sum_{a,b} \chi_{a,b} A_a \rho A_b^{\dagger}\]

where the \(A_{\alpha}\) are Pauli matrices. In the Schödinger picture, one would apply the quantum channels to the density matrix \(\rho\), but instead in the Heisenberg picture, the quantum channels are applied to the observable. The observable is stored in a Pauli tableau, \(<\mathcal{O}> = \sum_i c_i P_i\), which is simply a sparse representation of the observable in the Pauli basis, and applying the same quantum channel to a Pauli is simply done as:

\[\mathcal{E}(P) = \sum_{a,b} \chi_{a,b} A_b^{\dagger} P A_a\]

In general, this means that the number of Paulis in the sparse representation of the observable increases exponentially with the number of channels. However, there are some channels that have nicer properties from a computational standpoint.

Since Clifford gates map Paulis to Paulis, the quantum channel of a Clifford gate will do the same and not increase the size of the observable.

Additionally, a Pauli noise channel is a quantum channel whose chi-matrix is diagonal, meaning that it can be written as

\[\mathcal{E}(P) = \sum_{\alpha} \chi_{\alpha, \alpha} A_{\alpha}^{\dagger} P A_{\alpha} = \sum_{\alpha} (-1)^{\textrm{anticom}(A_{\alpha}, P)} \chi_{\alpha, \alpha} P\]

where \(\textrm{anticom}(A_{\alpha}, P) = 1\) if \(\{A_{\alpha}, P \} = 0\) and \(0\) otherwise. Therefore, a Pauli noise channel will not create new Paulis, meaning the size of the observable will be preserved. Instead, the already existing Paulis will be dampened by a coefficient \(c \approx (1-p)^k\) where \(k\) is the support of the Pauli undergoing the noise channel. This means that Paulis of larger weight are exponentially suppressed, making truncation based on a maximum weight all the more relevant [Shao2024].

To compensate for this exponential scaling, we can then apply several truncation methods to efficiently approximate the observable and the expectation value. For more informations on the four truncation modes we provide, please refer to our user guide on NoisySPD.

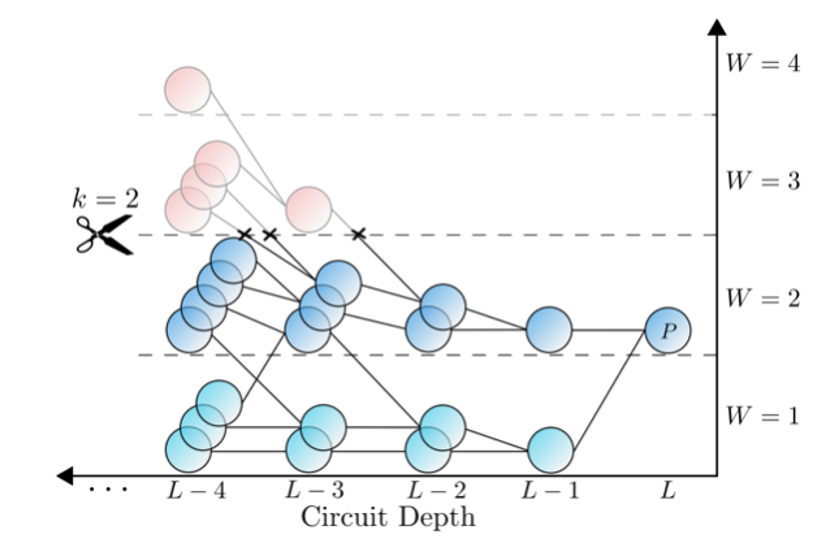
../../../_images/spd_doc_figure.png

Graphical representation of the evolution of an observable through Pauli propagation. Here, the main observable branches out into different Paulis as we run through the circuit in reverse order. Here, a truncation method based on the Hamming weight of the Paulis is applied, by truncating all the Paulis whose weight is above the given maximum W=2.

Specs and use-cases

Specs:

  • Accepts any type of gate and noise model, however decomposition into noise channel can be very costly for gates or large arity, so gates on up to 2 qubits are preferred.

  • Very efficient simulation of near-Clifford quantum circuits and/or Pauli noises (see use-cases below).

  • Accepts circuit with arbitrary connectivity.

  • Only computes expectation values of observables, samping cannot be performed.

Use cases:

  • Can simulate efficiently large circuits with high level of single-qubit Pauli noise [Shao2024].

  • Can simulate circuits with low-density of non-Clifford gates and with Pauli noise [Gonzalez2025].

Bibliography

[Shao2024] (1,2)

Shao, Y., Simulating Noisy Variational Quantum Algorithms: A Polynomial Approach. Phys. Rev. Lett. 133, 120603 (2024), https://arxiv.org/abs/2306.05804.

[Gonzalez2025]

González-García, G., Pauli path simulations of noisy quantum circuits beyond average case. Quantum 9, 1730 (2025), https://arxiv.org/abs/2407.16068.

[Martinez2025]

Martinez, V., Efficient simulation of parametrized quantum circuits under non-unital noise through Pauli backpropagation. https://arxiv.org/abs/2501.13050.

[Aharonov2023]

Aharonov, D., A Polynomial-Time Classical Algorithm for Noisy Random Circuit Sampling. In Proceedings of the 55th Annual ACM Symposium on Theory of Computing (STOC 2023), https://arxiv.org/abs/2211.03999.