Oracles and quantum types
When writing an oracle based quantum algorithm, such as Grover’s aglorithm, it is sometimes hard to translate a classical function implementing the oracle into a proper quantum circuit. Usually, this translation requires management of temporary resources and intermediate computations that can quickly become overwhelming (and, to be fair, not necessarily interesting).
PyAQASM comes with a nice feature that can help you efficiently describe complicated quantum oracles: high(er)-level quantum types.
It is possible, for instance, to declare a quantum register as a QInt. Quantum integers can then be used to directly perform arithmetic operations, or comparisons.
For instance, the following piece of code allocates two quantum integers and adds them:
from qat.lang import Program
from qat.lang.AQASM.qint import QInt
prog = Program()
qint1 = prog.qalloc(5, QInt)
qint2 = prog.qalloc(5, QInt)
qint1 += qint2
# Abstract circuit with some unimplemented adder
circuit_abs = prog.to_circ()
import qat.lang.AQASM.qftarith as qftarith
import qat.lang.AQASM.classarith as classarith
# Using QFT based adder
circuit_qft = prog.to_circ(link=[qftarith])
# Using carry based adder
circuit_class = prog.to_circ(link=[classarith])
In the following subsections, we detail the two quantum types implemented in pyAQASM: QBool and QInt.
Quantum booleans, quantum conditionals, and quantum oracles
The simplest quantum type is the QBool type (or QBoolArray for registers).
Allocation
Allocation can be done, as for any other type, by adding the corresponding type to the qalloc() or new_wires() method. Since registers are arrays of qubits, they can only be typed using the QBoolArray class.
from qat.lang.AQASM import Program, QRoutine
from qat.lang.AQASM.qbool import QBoolArray
prog = Program()
qbools = prog.qalloc(3, QBoolArray)
print(type(qbools))
print(type(qbools[0]))
# or
rout = QRoutine()
qbools = rout.new_wires(3, QBoolArray)
print(type(qbools))
print(type(qbools[0]))
<class 'qat.lang.AQASM.qbool.QBoolArray'>
<class 'qat.lang.AQASM.qbool.QBool'>
<class 'qat.lang.AQASM.qbool.QBoolArray'>
<class 'qat.lang.AQASM.qbool.QBool'>
Logical expressions
QBool can be composed using Python’s logical operators (AND, OR, NOT, XOR) to form boolean expressions:
from qat.lang.AQASM import QRoutine
from qat.lang.AQASM.qbool import QBoolArray
rout = QRoutine()
qbools = rout.new_wires(3, QBoolArray)
and_expr = qbools[0] & qbools[1] & qbools[2]
print(and_expr)
expr1 = qbools[0] & qbools[1] | qbools[2]
print(expr1)
expr2 = qbools[0] ^ qbools[1] | ~qbools[2]
print(expr2)
(q[0]&q[1]&q[2])
((q[0]&q[1])|q[2])
((q[0]^q[1])|(~ q[2]))
Evaluating expressions
How good is it to be able to construct expressions if we can’t use them?
Boolean expressions can be evaluated. Evaluating an expression will append a sequence of gates to the current scope (i.e the Program or the QRoutine in which the QBool were declared). This sequence of gates will evaluate the expression and output the result in a temporary qubit.
For instance the following code:
from qat.lang.AQASM import QRoutine
from qat.lang.AQASM.qbool import QBoolArray
rout = QRoutine()
qbools = rout.new_wires(3, QBoolArray)
expr2 = qbools[0] ^ qbools[1] | ~qbools[2]
output = expr2.evaluate()
print(rout.arity)
3
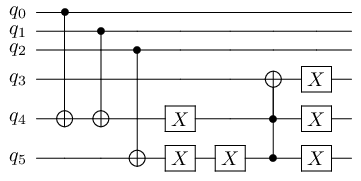
will produce the following circuit:
In this circuit, we have:
two CNOTs to compute the XOR of the first two qubits in some ancilla \(q_4\), (corresponding to the qbools[0] ^ qbools[1] term)
a CNOT and a X gate to compute the ~qbools[2] term in another ancilla \(q_5\)
5 X gates and a Toffoli gate to compute the final OR operator in \(q_3\), the output qubit. Here we use the de Morgan law to turn our OR into NOTS and a AND operator.
Note
Notice that, in this example, the produced routine has arity 3. Indeed, the qubit used in the .evaluate method are automatically flagged as ancillae. Keep that in mind when using the .evaluate method.
It is also possible to specify an output qubit for the evaluation procedure:
from qat.lang.AQASM import QRoutine
from qat.lang.AQASM.qbool import QBoolArray
rout = QRoutine()
qbools = rout.new_wires(3, QBoolArray)
output = rout.new_wires(1)
expr2 = qbools[0] ^ qbools[1] | ~qbools[2]
expr2.evaluate(output=output)
print(rout.arity)
4
will produce the same circuit, but this time the routine will have arity 4 since output was declared as a proper input of the routine.
Quantum conditionals and with statements
Expressions can also be combined with a with statement to produce a context in which the expression is evaluated. For instance, the following piece of code evaluates an expression in a with statement and copies the result of the evaluation in an output qubit.
from qat.lang.AQASM import QRoutine, CNOT
from qat.lang.AQASM.qbool import QBoolArray
rout = QRoutine()
qbools = rout.new_wires(3, QBoolArray)
output = rout.new_wires(1)
expr2 = qbools[0] ^ qbools[1] | ~qbools[2]
with expr2 as condition:
CNOT(condition, output)
print(output[0], condition[0])
q[3] q[4]
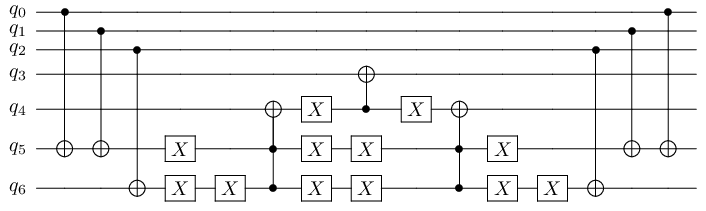
This will produce the following circuit:
Notice that the boolean expression was first evaluated in a temporary qubit (qubit 4), then we copied the result in an output qubit (qubit 3), finally, the expression was uncomputed upon exiting the with block.
The with statement is in fact just a syntactic sugar for the following code:
from qat.lang.AQASM import QRoutine, CNOT
from qat.lang.AQASM.qbool import QBoolArray
rout = QRoutine()
qbools = rout.new_wires(3, QBoolArray)
output = rout.new_wires(1)
expr2 = qbools[0] ^ qbools[1] | ~qbools[2]
# starting a compute scope
with rout.compute():
# evaluating the expression
condition = expr2.evaluate()
# copying the result
CNOT(condition, output)
# uncomputing the evaluation
rout.uncompute()
# releasing the ancilla `condition` for later use
rout.free_ancillae(condition)
Warning
Quantum conditionals cannot be called on an expression whose underlying qubits were allocated in a Program class.
Therefore, it should only be used inside a QRoutine first.
Building phase oracles
Last but not least, it is possible to use a boolean expression to automatically generate a quantum circuit that will flip the phase of basis states that verify the expression. This is done by calling the method phase on an expression.
from qat.lang.AQASM import Program, CNOT, H
from qat.lang.AQASM.qbool import QBoolArray
prog = Program()
qbools = prog.qalloc(2, QBoolArray)
for qbit in qbools:
H(qbit)
expr = qbools[0] & qbools[1]
expr.phase()
job = prog.to_circ().to_job()
from qat.qpus import get_default_qpu
result = get_default_qpu().submit(job)
for sample in result:
print(sample.state, sample.amplitude)
|[False, False]> (0.4999999999999999+0j)
|[False, True]> (0.4999999999999999+0j)
|[True, False]> (0.4999999999999999+0j)
|[True, True]> (-0.4999999999999999+0j)
Since our expression evaluates at True if and only if the two qubits are set to True only state \(|11\rangle\) had its phase flipped.
Warning
The phase method cannot be called on an expression whose underlying qubits were allocated in a Program class.
Therefore, it should only be used inside a QRoutine first.
Quantum integers
The second type allows to type registers as quantum integers.
Allocation
Similarly to QBool, QInt is allocated using the qalloc() or new_wires() methods.
from qat.lang.AQASM import Program, QRoutine
from qat.lang.AQASM.qint import QInt
prog = Program()
qint = prog.qalloc(5, QInt)
print(qint)
rout = QRoutine()
qint = rout.new_wires(5, QInt)
print(qint)
QInt(q[0]..q[4])
QInt(q[0]..q[4])
Setting a classical value
QInt has a method called set_value() that XORS the content of the QInt with a classical value.
from qat.lang.AQASM import QRoutine
from qat.lang.AQASM.qint import QInt
rout = QRoutine()
qint = rout.new_wires(2, QInt)
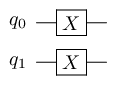
qint.set_value(3)
produces:
Arithmetic expressions
Instances of QInt can be combined via addition and multiplication. Combining them forms an arithmetic expression without adding any gate to the underlying circuit.
The only operation that triggers a circuit generation is the += operator.
from qat.lang.AQASM import Program, QRoutine
from qat.lang.AQASM.qint import QInt
prog = Program()
qint1 = prog.qalloc(5, QInt)
qint2 = prog.qalloc(5, QInt)
qint1 + qint2
circuit1 = prog.to_circ()
qint1 += qint2
circuit2 = prog.to_circ()
print("First circuit")
for op in circuit1.iterate_simple():
print(op)
print("Second circuit")
for op in circuit2.iterate_simple():
print(op)
First circuit
Second circuit
('ADD', [5, 5], [4, 3, 2, 1, 0, 9, 8, 7, 6, 5])
Notice that the first circuit is empty: the statement qint1 + qint2 did not produce any gate. The second statement, qint1 += qint2 did produce an adder.
The same holds for multiplication:
from qat.lang.AQASM import Program, QRoutine
from qat.lang.AQASM.qint import QInt
prog = Program()
qint1 = prog.qalloc(5, QInt)
qint2 = prog.qalloc(5, QInt)
qint3 = prog.qalloc(5, QInt)
qint1 * qint2
circuit1 = prog.to_circ()
qint3 += qint1 * qint2
circuit2 = prog.to_circ()
print("First circuit")
for op in circuit1.iterate_simple():
print(op)
print("Second circuit")
for op in circuit2.iterate_simple(depth=0):
print(op)
First circuit
Second circuit
('MULT', [5, 5, 5], [4, 3, 2, 1, 0, 9, 8, 7, 6, 5, 14, 13, 12, 11, 10])
Conditionals on quantum integers
It is possible to compare quantum integers with one another or to some classical values. These comparisons produce QBool objects and can thus be used to produce oracles or conditional statements.
For instance, one can write a program that:
compares two quantum integers
and increments a quantum integer if and only if the comparison fails
from qat.lang.AQASM import QRoutine
from qat.lang.AQASM.qint import QInt
rout = QRoutine()
qint1 = rout.new_wires(5, QInt)
qint2 = rout.new_wires(5, QInt)
qint3 = rout.new_wires(5, QInt)
with qint1 != qint2 as condition:
qint3 += condition.cast_to(QInt)
Notice the usage of the cast_to method that allows us to cast any type to a new type (by re-wrapping the quantum register).
Of course, one can also use the .evaluate and .phase methods. For instance, the following piece of code flips the phase of all classical states that represent integers below some constant, say 5:
from qat.lang.AQASM import Program, QRoutine, H
from qat.lang.AQASM.qint import QInt
import qat.lang.AQASM.qftarith as qftarith
rout = QRoutine()
qint = rout.new_wires(3, QInt)
for qbit in qint:
H(qbit)
(qint < 5).phase()
prog = Program()
qbits = prog.qalloc(3, QInt)
rout(qbits)
circuit = prog.to_circ(link=[qftarith])
job = circuit.to_job()
from qat.qpus import get_default_qpu
result = get_default_qpu().submit(job)
for sample in result:
print(sample.state, sample.amplitude)
|0>|Anc:0> (-0.35355339059327323+1.23913020889862e-16j)
|1>|Anc:0> (-0.3535533905932733+4.8658288018013407e-17j)
|2>|Anc:0> (-0.3535533905932733+1.0995513354634973e-16j)
|3>|Anc:0> (-0.35355339059327323+4.190703022179928e-17j)
|4>|Anc:0> (-0.35355339059327345+6.402318085305039e-17j)
|5>|Anc:0> (0.35355339059327295-1.6007773964406963e-16j)
|6>|Anc:0> (0.35355339059327306-1.189616927591931e-16j)
|7>|Anc:0> (0.35355339059327306-1.2041754338276273e-16j)
Example: Grover oracle for graph coloring
Using these tools, it is quite straightforward to write simple phase oracles for Grover-like applications.
For instance, one can write in a few lines of code a routine that will act as an oracle for a graph coloring problem.
We will construct a Python function that will take a graph (networkx.Graph) and a number of bits to use to store each color. It will return a QRoutine that flips the phase of a basis state if and only if it describes a clean coloration.
from functools import reduce
from qat.lang.AQASM import QRoutine
from qat.lang.AQASM.qint import QInt
def coloring_oracle(graph, bitlength):
rout = QRoutine()
colors = [rout.new_wires(bitlength, QInt) for _ in graph.nodes()]
reduce(
lambda a, b: a & b,
(colors[a] != colors[b] for a, b in graph.edges())
).phase()
return rout
import networkx as nx
graph = nx.generators.path_graph(20)
bitlength = 1 # looking for 2 colorings, so colors are stored on a single bit
oracle = coloring_oracle(graph, bitlength)
print("Oracle has arity:", oracle.arity)
print("Oracle uses {} ancillae".format(len(oracle.ancillae)))
Oracle has arity: 20
Oracle uses 19 ancillae
In this function, we:
declare an array of quantum integers, one for each vertex of our graph
build a formula that compute the logical and of \(c_i \neq c_j\) for each edge \(i\) \(j\) of our graph
use this formula to perform a phase flip
This implementation uses a lot of qubits. For each \(c_i \neq c_j\) in our for loop, pyAQASM allocates a temporary qubit. Then a generalized controlled \(Z\) is used to flip the phase of the states that have all these ancillae set to 1. Finally, all the temporary qubits are freed by uncomputing the \(c_i \neq c_j\) statements.
Asymptotically, this oracle uses \(b|V| + |E|\) qubits, without considering the fact that the implementation of the generalized controlled \(Z\) might require additional qubits.
It is possible to save up some qubits, at the cost of an increased number of gates. The following code snippet implements the same oracle, but a bit differently:
it allocates a counter large enough to count up to \(|E|\)
for each edge, if \(c_i \neq c_j\), it increments the counter by 1
it flips the phase of the basis state if and only if the counter contains exactly \(|E|\)
finally, it uncomputes all the counter increments
from qat.lang.AQASM import QRoutine
from qat.lang.AQASM.qint import QInt
def coloring_oracle(graph, bitlength):
rout = QRoutine()
colors = [rout.new_wires(bitlength, QInt) for _ in graph.nodes()]
counter = rout.new_wires(graph.number_of_edges().bit_length(), QInt)
with rout.compute():
for a, b in graph.edges():
with colors[a] != colors[b] as condition:
counter += condition.cast_to(QInt)
(counter == graph.number_of_edges()).phase()
rout.uncompute()
rout.set_ancillae(counter)
return rout
import networkx as nx
graph = nx.generators.path_graph(20)
bitlength = 1 # looking for 2 colorings, so colors are stored on a single bit
oracle = coloring_oracle(graph, bitlength)
print("Oracle has arity:", oracle.arity)
print("Oracle uses {} ancillae".format(len(oracle.ancillae)))
Oracle has arity: 20
Oracle uses 6 ancillae
Asymptotically, this oracle is far more frugal since it uses only \(b|V| + log(|E|)\) qubits.
Notice that in both examples, we didn’t have to directly mention any quantum gate. Everything is handled by the quantum types.