MPO: Matrix Product Operator-based quantum simulator
Note
For more information on entanglement-aware simulations, see our article.
Matrix product-based tensor networks methods have been among the most popular avenue at circumventing the exponential scaling of exact quantum simulations [Vidal03] [Schollwoeck2010]. Lowly entangled states can be efficiently simulated using matrix product states. This approach has allowed the reach of systems sizes far beyond what exact computations can achieve.
Any mixed state can be represented as a matrix product operator (MPO) [Schollwoeck2010]. The density matrix of a quantum state of \(N\) qubits is cast into a factorized form of \(N\) tensors connected to each other with what is generally called bond dimension. Physically, bond dimensions can be thought of as the amount of entanglement a quantum state can encapsulate. Contracting every tensors of this MPO along its bond dimensions gives back the quantum state in its standard density matrix representation. But where the MPO representation really shines is at approximating large quantum states into a more compact version, by truncating bond dimensions. This is done by limiting bond dimensions growth up to a pre-defined maximum bond dimension, which effectively approximates the quantum state. The more entanglement, the bigger the truncation errors, which limits MPO effectiveness to lowly entangled, but possibly very large quantum states.
Truncating bond dimensions higher than a specific maximum bond dimension is the standard approach when it comes to approximating MPS. However a new technique called entanglement-aware has been designed at Qaptiva™ [Oliva2023]. This algorithm fully leverages the presence or absence of both noise and entanglement. It dynamically adapts the bond dimensions of the quantum state throughout the simulation, based on an input fidelity the quantum state has to at least reach. Decreasing (resp. increasing) the desired fidelity decides how aggressive (resp. conservative) the algorithm will be at truncating bond dimensions.
As noise tend to destroy quantum coherences, EA-MPO is especially powerful at dealing with highly noisy quantum systems. It can adapt the bond dimensions to the local entanglement needs throughout the simulation and proves vastly superior to standard maximum bond dimension MPO.
Since bond dimensions are kept as low as possible for every operation, the algorithm efficiency far surpasses that of regular fixed maximum bond dimensions algorithms, while simultaneously allowing trustworthy output quantum states. In particular, a noiseless random circuit of 300 qubits and depth 25 simulated using MPO methods takes one week of computation time, while EA-MPO only needs 40 minutes to reach similar quantum state fidelity.
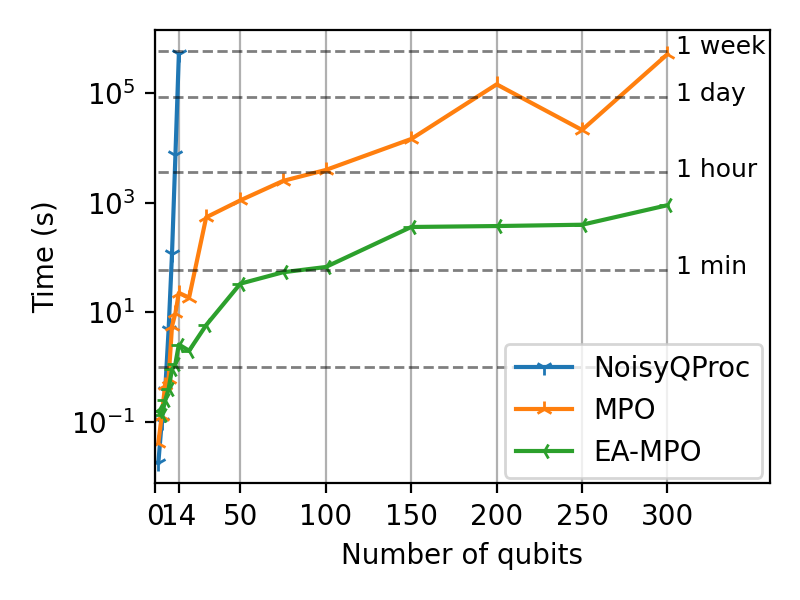
Comparison of the simulation time between MPO and EA-MPO on random circuits of depth 25. For each point, the MPO maximum bond dimension is taken as the maximum bond dimension encountered during the EA-MPO simulation. Both quantum state fidelities are equal.
qat.qpus.MPO QPU implements both truncation techniques. Please see
our notebook on MPO and EA-MPO simulations for more informations on how to use
the qat.qpus.MPO QPU.
If you wish to use MPO tensor networks directly, refer to our notebook about MPS and MPO computation and usage.