MPS: Matrix Product State-based quantum simulator

Note

For more information on entanglement-aware simulations, see our article.

Matrix product-based tensor networks methods have been among the most popular avenue at circumventing the exponential scaling of exact quantum simulations (see [Vidal03] or [Schollwoeck2010]). Lowly entangled states can be efficiently simulated using matrix product states. This approach has allowed the reach of systems sizes far beyond what exact computations can achieve.

Any pure state can be represented as a matrix product state (MPS). The state vector of a quantum state of \(N\) qubits is cast into a factorized form of \(N\) tensors connected to each other with what is generally called bond dimension. Physically, bond dimensions can be thought of as the amount of entanglement a quantum state can encapsulate. Contracting every tensors of this MPS along its bond dimensions gives back the quantum state in its standard state vector form. But where the MPS representation really shines is at approximating large quantum states into a more compact version, by truncating bond dimensions. This is done by limiting bond dimensions growth up to a pre-defined maximum bond dimension, which effectively approximates the quantum state. The more entanglement, the bigger the truncation errors, which limits MPS effectiveness to lowly entangled, but possibly very large quantum states.

Truncating bond dimensions higher than a specific maximum bond dimension is the standard approach when it comes to approximating MPS. However a new technique called entanglement-aware has been designed at Qaptiva™ [Oliva2023]. This algorithm dynamically adapts the bond dimensions of the quantum state throughout the simulation, based on an input fidelity the quantum state has to at least reach. Decreasing (resp. increasing) the desired fidelity decides how aggressive (resp. conservative) the algorithm will be at truncating bond dimensions.

Since bond dimensions are kept as low as possible for every operation, the algorithm efficiency far surpasses that of regular fixed maximum bond dimensions algorithms, while simultaneously allowing trustworthy output quantum states. In particular, a noiseless random circuit of 300 qubits and depth 75 simulated using MPS methods takes one week of computation time, while EA-MPS only needs 2 hours to reach similar quantum state fidelity.

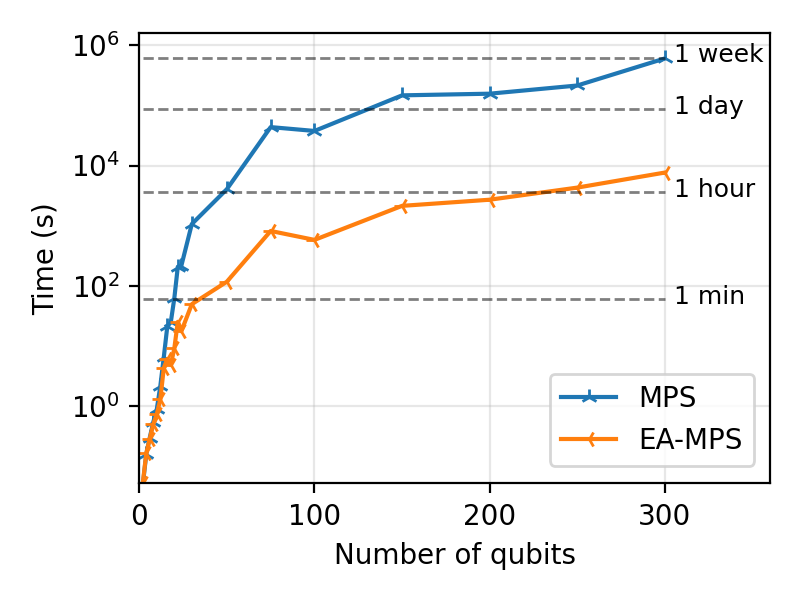
Comparison of the simulation time between MPS and EA-MPS on random circuits of depth 75. For each point, the MPS maximum bond dimension is taken as the maximum bond dimension encountered during the EA-MPS simulation. Both quantum state fidelities are equal.

qat.qpus.MPS QPU implements both truncation techniques. Please see our notebook on MPS and EA-MPS simulations for more informations on how to use the qat.qpus.MPS QPU.

If you wish to use MPS tensor networks directly, refer to our notebook about MPS and MPO computation and usage.

See the mathematical description here.