qat.lang

This module provides a powerful API to create quantum circuits. Quantum circuits can be composed of quantum gates (including user defined gates), intermediate measurements, classically controlled gates, etc.

Programming tools

This module provide tools to create advanced quantum circuit. Designed quantum circuit is detailed in the user guide, section gate-based programming

`qat.lang.Program`	Program class, to create quantum circuit
`qat.lang.qfunc()`	qfunc decorator, to define a gate-based quantum function
`qat.lang.qrout()`	qrout decorator, to define a circuit using a function

Gate structures

All classes describing unitary operators inherit from the Gate class.

`qat.lang.AbstractGate`	User defined gate
`qat.lang.build_gate()`	Decorator creating a quantum gate
`qat.lang.QRoutine`	Subcircuit behaving as a gate object
`qat.lang.AQASM.gates.Gate`	Parent class for all quantum gates / unitary operators
`qat.lang.AQASM.gates.ParamGate`	Parametrized gate

Quantum types

Quantum boolean and expressions

`qat.lang.AQASM.qbool.QBool`	Quantum bool
`qat.lang.AQASM.qbool.QBoolArray`	Array of quantum bool
`qat.lang.AQASM.qbool.QClause`	Quantul clause

Quantum integers

`qat.lang.AQASM.qint.QArithExp`	Arithmetic expression
`qat.lang.AQASM.qint.QCompExp`	Comparison expression
`qat.lang.AQASM.qint.QInt`	Quantum integer

Managing registers

`qat.lang.AQASM.bits.BoolFormula`	Clasical formula
`qat.lang.AQASM.bits.Cbit`	Classical bit class
`qat.lang.AQASM.bits.CRegister`	Register of cbits
`qat.lang.AQASM.bits.Qbit`	Quantum bit class
`qat.lang.AQASM.bits.QRegister`	Register of qubits

Gate set management

qat.lang.AQASM.misc.generate_gate_set()

Gate set generator

Linker and low level circuit manipulation

In pyAQASM, gates can be specified using various representations. They can be purely abstract (a name and a set of parameter values, such as RZ, [PI/2]). To this abstract syntax, one can attach a matrix, or even a subcircuit that implements this gate (this is the case of adders of the arithmetic library for instance).

Circuits are generated in two steps:

first a skeleton of the circuit is generated (for instance adders will be gates called ADD in this skeleton)

then a subcircuit is generated and attached to this abtract gate.

This second step is handled by a class called Linker. It can be useful in some settings to manipulate this Linker object in order to replace gates by subcircuits, or to generate matrices in order to simulate the circuit.

qat.lang.linking.Linker

pyAQASM linker

Quantum labraries and basic algorithms

This module provides a set of routine to simplify the implementation of quantum circuits

Arithmetic routines

pyAQASM comes with a pre-implemented set of arithmetic routines. Since there are different approaches to implement arithmetic routines, we provide various implementation of some low-level routines such as additions and additions by a classical constant. Higher level routines are then implemented by calling some implementation of these lower level routines.

The following diagram sums up the various routines and their implementation. Arrows mean “uses”, green boxes indicates the implementation strategy:

QFT means QFT-based arithmetic

CARRY means ripple-carry based arithmetic

INDEP means agnostic. These routines call lower level routines, indepentently from their implementation.

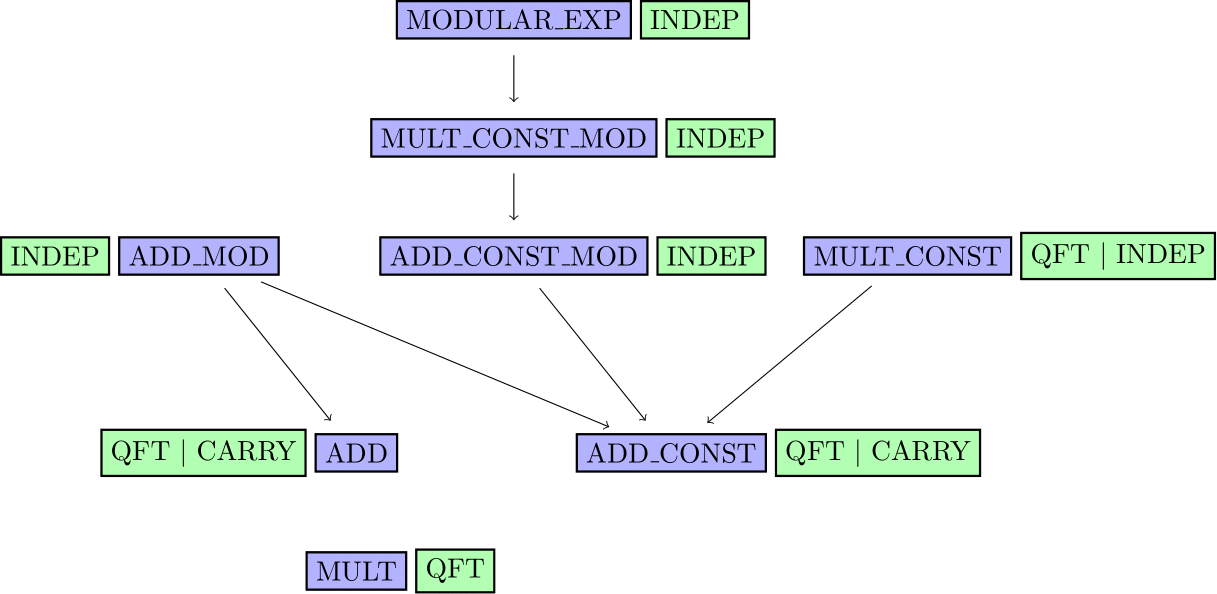
The routines are separated into three distinct namespaces according to these three types of implementation strategy: QFT, CARRY, INDEP.

Warning

All methods are decorated using @build_gate which turn them into AbstractGates. To access the underlying routine instead of the wrapping gates, the method name can be prefixed with ‘~’.

# will generate a call to an AbstractGate having the QFT as circuit
# implementation
QFT(3)

# will generate a QRoutine object
(~QFT)(3)

The two behaviors are comparable, except that using the U notation allows to skip the inlining step when extracting the circuit (.to_circ method with inline=False) and to link another implementation of gate U later on. Using (~U) will effectively inline the gate no matter what

State preparatation and QRAM

qat.lang.models.KPTree

A class representing a Kerinidis-Prakash tree for a QRAM

Algorithms

There are a few basic algorithms present in the qat.lang.algorithms module:

`qat.lang.algorithms.amplification_step()`	Single amplification step of Grover’s algorithm
`qat.lang.algorithms.phase_estimation()`	Phase estimation routine
`qat.lang.algorithms.quantum_counting()`	Performs a quantum counting on some oracle

Additionally, the submodule qat.lang.algorithms.amplification contains some functions that might be useful:

`qat.lang.algorithms.amplification.grover_diffusion()`	Grover diffusion
`qat.lang.algorithms.amplification.householder()`	Performs a Householder for any unitary
`qat.lang.algorithms.amplification.uniform_distribution()`	Prepare a uniform distribution from state \(\|0...0\rangle\)