Problem generators

Qaptiva provides batch generators used to both generate a quantum job (used to solve a combinatorial problem) and parse the result to return a user-friendly structure.

These batch generators can generate different types of job, to be compatible with different types of QPUs. The different types of jobs are:

These jobs are generated using the method qaoa_job() of CircuitGenerator by passing job_type="qaoa" to the constructor of the generator and are designed to be executed on a digital QPU. Two jobs will be submitted to the QPU:

  1. a variational job to determine the best parameters

  2. a sampling job to find an actual solution to the combinatorial problem

For instance, the following example uses MaxCutGenerator to generate jobs solving the NP-Hard problem Max Cut on a graph given to this generator:

import networkx as nx
from qat.generators import MaxCutGenerator

graph = nx.full_rary_tree(3, 6)

# The job_type here can also be "aqo" or "sqa"
batches = MaxCutGenerator(job_type="qaoa").generate(None, graph)

This generator can be piped to a computation stack of plugins and a QPU, creating an Application. The Max Cut problem can then be solved by calling the execute() method.

import networkx as nx
from qat.generators import MaxCutGenerator
from qat.plugins import ScipyMinimizePlugin
from qat.qpus import get_default_qpu

graph = nx.full_rary_tree(3, 6)

max_cut_application = (
        MaxCutGenerator(job_type="qaoa")
        | ScipyMinimizePlugin(method="COBYLA", tol=1e-5, options={"maxiter": 200})
        | get_default_qpu()
)
combinatorial_result = max_cut_application.execute(graph)

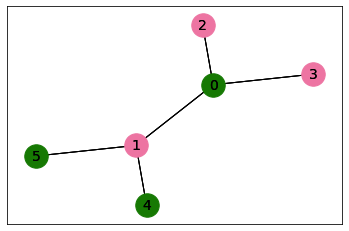
print(combinatorial_result.subsets)
print(combinatorial_result.cost)

[[0, 4, 5], [1, 2, 3]]
-5.0

The parsed combinatorial result can also be displayed with NetworkX:

combinatorial_result.display()
../_images/max_cut_generator_result.png

These jobs are generated using the method to_job() of Ising by passing job_type="sqa" to the constructor of the generator and are designed to be executed with SQAQPU.

For instance, the following example uses MaxCutGenerator to generate jobs solving the NP-Hard problem Max Cut on a graph given to this generator:

import networkx as nx
from qat.generators import MaxCutGenerator

graph = nx.full_rary_tree(3, 6)

# The job_type here can also be "qaoa" or "aqo"
batches = MaxCutGenerator(job_type="sqa").generate(None, graph)

This generator can be piped to a computation stack of plugins and a QPU, creating an Application. The Max Cut problem can then be solved by calling the execute() method.

import networkx as nx
from qat.generators import MaxCutGenerator
from qat.qpus import SQAQPU

graph = nx.full_rary_tree(3, 6)

max_cut_application = (
        MaxCutGenerator(job_type="sqa")
        | SQAQPU()
)
combinatorial_result = max_cut_application.execute(graph)

print(combinatorial_result.subsets)
print(combinatorial_result.cost)

[[1, 2, 3], [0, 4, 5]]
-5.0

The parsed combinatorial result can also be displayed with NetworkX:

combinatorial_result.display()
../_images/max_cut_generator_result.png

These jobs are generated by passing job_type="aqo" to the constructor of the generator and are designed to be executed on an analog QPU (or job_type="ryd" for Rydberg atom QPU).

For instance, the following example uses MaxCutGenerator to generate jobs solving the NP-Hard problem Max Cut on a graph given to this generator:

import networkx as nx
from qat.generators import MaxCutGenerator

graph = nx.full_rary_tree(3, 6)

# The job_type here can also be "qaoa" or "sqa"
batches = MaxCutGenerator(job_type="aqo").generate(None, graph)

This generator can be piped to a computation stack of plugins and a QPU, creating an Application. The Max Cut problem can then be solved by calling the execute() method.

import networkx as nx
from qat.generators import MaxCutGenerator
from qat.qpus import AnalogQPU

graph = nx.full_rary_tree(3, 6)

max_cut_application = (
        MaxCutGenerator(job_type="aqo")
        | AnalogQPU()
)
combinatorial_result = max_cut_application.execute(graph)

print(combinatorial_result.subsets)
print(combinatorial_result.cost)

[[0, 4, 5], [1, 2, 3]]
-5.0

The parsed combinatorial result can also be displayed with NetworkX:

combinatorial_result.display()
../_images/max_cut_generator_result.png

NP-hard problems generators

Max Cut generator
Graph Partitioning generator
K-Clique generator
Vertex Cover generator
Graph Colouring generator