High-level optimization
The qat.pbo module provides different tools to optimize a quantum
circuit using rule-based rewriting. This page presents a high-level
optimization tool, PatternManager. On this page, only
simple patterns are used. Nevertheless, this tool accepts complex
patterns: to learn more about patterns, please refer to Writing patterns.
The notebook Circuit optimization using PatternManager
may help to better understand our syntax to describe a pattern, and how to use
a pattern with PatternManager plugin.
This notebook tries to minimize the depth of a QAOA
circuit using commutation rules defined by a set of patterns.
Introduction
The class PatternManager is a plugin used to replace
patterns automatically. Rewriting rules are applied to maximize a
score function defined by the user. Patterns are grouped, each group being
composed of equivalent patterns (a pattern can be replaced by any pattern
of the same group).
For instance, the following two patterns are equals. A group composed of these two patterns could be defined.
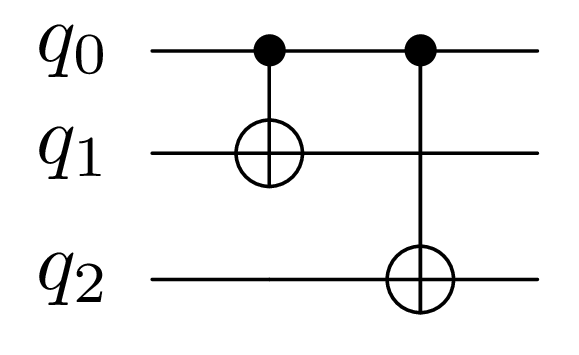
|

|
This code can be used to define a group composed of these two patterns.
from qat.plugins import PatternManager
# Define manager
manager = PatternManager()
# Create group
group = manager.new_group()
group.add_pattern([("CNOT", [0, 1]), ("CNOT", [0, 2])])
group.add_pattern([("CNOT", [0, 2]), ("CNOT", [0, 1])])
The optimizer is allowed to replace a pattern by any pattern of the same group.
The pattern [("CNOT", [0, 1]), ("CNOT", [0, 2])] can be replaced by
the pattern [("CNOT", [0, 2]), ("CNOT", [0, 1])] and vice-versa.
Behavior of the optimizer
This optimizer has two types of optimization. These optimization types are combined (these two optimizations are performed simultaneously) and are:
local optimization: this optimization is used to optimize a sub-circuit (each sub-circuit is replaced by an equivalent sub-circuit strictly better)
global optimization: this optimization is used to optimize the whole circuit
Since PatternManager is a high-level optimizer, metrics
(or score functions) could be set to allow the optimizer to select
rules to apply. There are two kind of metrics (one metric per optimization
type):
local_metric (optional): this function takes a circuit and returns a score. This function is used to select best patterns for each group. Each pattern is replaced by a pattern (of the same group) having a better local score.
global_metric (optional): this function takes a circuit and returns a score. This optimizer will apply rules to maximize this metric. This function is used to compare two circuits.
Warning
Please use the local_metric if and only if each pattern can be
trivially cast into a Circuit (i.e. if the pattern
is not composed of abstract name neither abstract register).
See the next section, Advanced optimization for more details concerning the meaning and use of these metrics.
Flagging patterns to remove
If a pattern is trivially worse than other patterns of its group, this pattern
can be flagged with pattern_to_remove().
The optimizer will always replace this pattern by a non-flagged pattern of the
same group.
For instance, defining a plugin which remove patterns composed of two
"H" gates can be done using few lines of code.
from qat.plugins import PatternManager
# Define manager
manager = PatternManager()
# Define group
group = manager.new_group()
group.add_pattern([])
group.pattern_to_remove([("H", [0]), ("H", [0])])
# The plugin "manager" removes H - H patterns.
The plugin "manager" is composed of a single group composed of two
patterns. One of these patterns (the \(H - H\) pattern) is clearly worse
than the other one, so this plugin will replace each occurrence of the worse
pattern by the best equivalent pattern (here []).
Advanced optimization
Metrics should be used to perform non-trivial optimization. A global metric is used to optimize the whole circuit by doing local changes. A local metric can be used to force some rewriting rules.
Warning
A local metric allows the optimizer to select quickly the best patterns
in a group. Since the use of a local metric imposes extra constraints
on patterns (patterns should be trivially castable into circuit),
the use of PatternManager may become harder. If
you know which pattern is the best one, please rather use
the method add_pattern() to
add an optimal pattern in a group and the method
pattern_to_remove() to
add a non-optimal pattern in a group.
Since the corresponding optimization problem is hard to solve, one has to resort to heuristics. Two heuristics have been implemented in this module. They are valid for any circuit:
“annealing”: a simulated annealing is used to optimize the circuit
“gradient”: a gradient descent is used to optimize the circuit
Example of an optimization: circuit execution time
In this section, an example of optimization is given. As a global metric, we take the overall execution time of the circuit.
The following circuit will be optimized. We assume that the duration of computation of any quantum gate is 1 unit of time. The duration of our circuit is then 3 units of time.
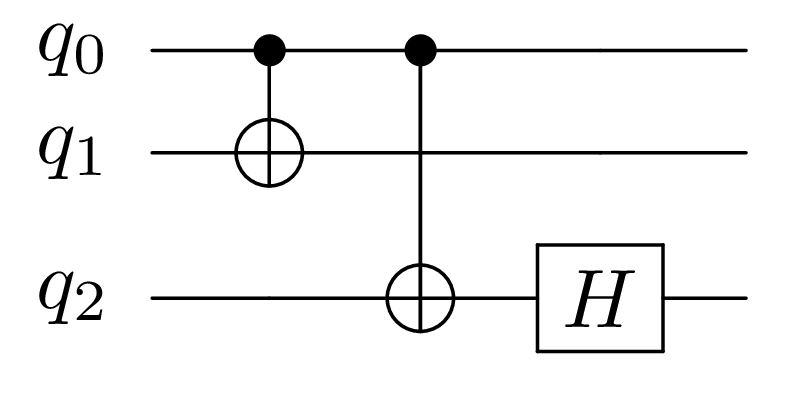
The class PatternManager may be used to optimize this
program by doing permutation between gates. Since two CNOT gates can commute
if these gates share the same control qubit, the following group may be
defined (group of two equivalent patterns):

|

|
Using this rule, our optimizer can perform local changes to get the following optimal circuit (the duration has been reduced to 2 units of time):
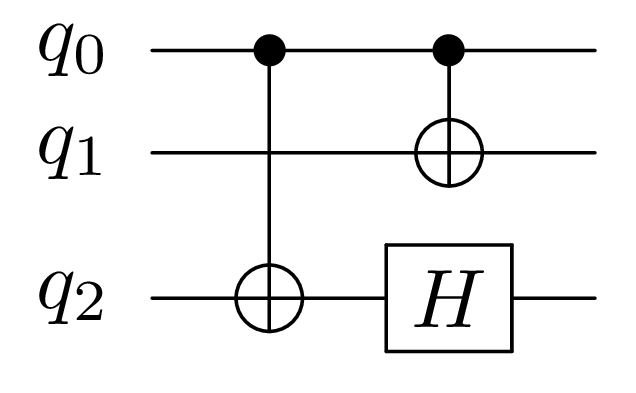
Implementation of the example
Here, it just happens that the overall duration metric is already implemented
in qat.nnize (this because qat-nnize tries to minimize the same metric
when inserting SWAP gates), so we will import it from there.
Since the goal of this optimization is to minimize the duration of the circuit, the metric will compute the opposite of the duration (so the goal of this optimization is to maximize this metric).
The optimization can then be done using only few lines of code:
First, we define our non-optimal circuit using the qat.lang module.
from qat.lang.AQASM import Program, CNOT, H
from qat.plugins import PatternManager
from qat.nnize.metrics import DurationMetric
#
# Defining program
#
prog = Program()
qbits = prog.qalloc(3)
prog.apply(CNOT, qbits[0], qbits[1])
prog.apply(CNOT, qbits[0], qbits[2])
prog.apply(H, qbits[2])
circ = prog.to_circ()
Then, we define a metric. The optimizer will have to maximize this metric. We can check that our initial circuit has a duration of 3 units of time.
#
# Define metric to minimize overall time
#
# Define metric
metric = DurationMetric()
# Set duration of each gate equal to 1 unit of time
metric.set_gate_time({"-DEFAULT-": 1})
# Adapt metric to minimize duration of the circuit
metric.minimize_overall_time()
Finally, we define an optimizer to minimize the overall duration of our circuit. Our optimizer is composed of a metric and of a group of two equivalent patterns. The optimizer will use this rule to maximize our metric (i.e. minimize the duration of the circuit).
#
# Define optimizer
#
manager = PatternManager(global_metric=metric)
# Define group
group = manager.new_group()
group.add_pattern([("CNOT", [0, 1]), ("CNOT", [0, 2])])
group.add_pattern([("CNOT", [0, 2]), ("CNOT", [0, 1])])
# Optimize
opt_circ = manager.replace_pattern(circ)
print("Final duration: %d" % -metric(opt_circ))
The circuit has been optimized.