qat.qpus.MPSLegacy

class qat.qpus.MPSLegacy(lnnize=False, no_merge=False, threshold=None, n_trunc=None, plugins=None, disable_resource_management=False)

Circuit simulator based on a Matrix Product State representation.

Parameters

  • lnnize (bool, optional) – use MPS built-in nnizer to make circuit 1D-linear-nearest-neighbor, if needs be. If you are hunting for performance, consider lnnizing with the optimized module qat.nnize instead.

  • no_merge (bool, optional) – Activation of MPS pre-simulation merging of gates. By default, consecutive gates are merged whenever possible. This merging has been shown to reduce execution time in most cases.

  • threshold (float, optional) – specify threshold below which Schmidt coefficients are truncated.

  • n_trunc (float, optional) – maximum bond dimension of the MPS.

  • disable_resource_management (bool, optional) – since evaluating the true memory requirement of qat-mps is a very difficult problem, our current memory model will sometimes reject a legitimate computation. Setting disable_resource_management to True allows to override the model, at the cost of losing guarantees about memory.

Mathematical description

This simulator represents the quantum state in the form of a matrix product state (MPS):

\[|\psi\rangle=\sum_{i_{1},\dots,i_{N}\in \{0,1\}^{N}}M^{1,i_{1}}M^{2,i_{2}}\cdots M^{N,i_{N}}|i_{1}\dots i_{N}\rangle\]

where \(\{M^{k,i_{k}}\}_{k=1\dots N}\) are matrices, with respective dimensions \(\left(\chi_{_{k-1}}, \chi_{_{k}}\right)\), consistent with matrix multiplication.

The \(\{\chi_{_{k}}\}_{k=1 \dots N}\) are called the bond dimensions. At the beginning of the simulation, with the state \(|0...0\rangle\), they are all equal to 1.

At all times, \(\chi_{_{0}} = \chi_{_{n}} = 1\).

The other bond dimensions can vary anywhere from 1 to exponentially large values, depending on the amount of entanglement within the system.

In fact, as a rule of thumb, if \(\mathcal{S}\) is the entanglement (von Neumann entropy of entanglement) of a state, then the maximum bond dimension will be of the order [Schollwoeck2010]

\[\chi\sim2^{\mathcal{S}}\]

The simulation of slightly entangled quantum computations using MPS was first described by Guifré Vidal in [Vidal03]. Matrix Product States are a special case of tensor network states [Orus2014]. One could say that, within the MPS formulation, information has been relocalized into qubit-specific tensors, through factorization of the entire state vector. See [Vidal03] for more details.

The figure below gives the description of an MPS in the pictorial language of tensor networks, as a 1D-chain of rank-3 tensors: \(\{M^{k}\}_{k=1\dots N}\). For the sake of comparison, we also give the diagram corresponding to an entire amplitude vector, as used in the linalg simulator. (it is just a huge rank-N tensor)

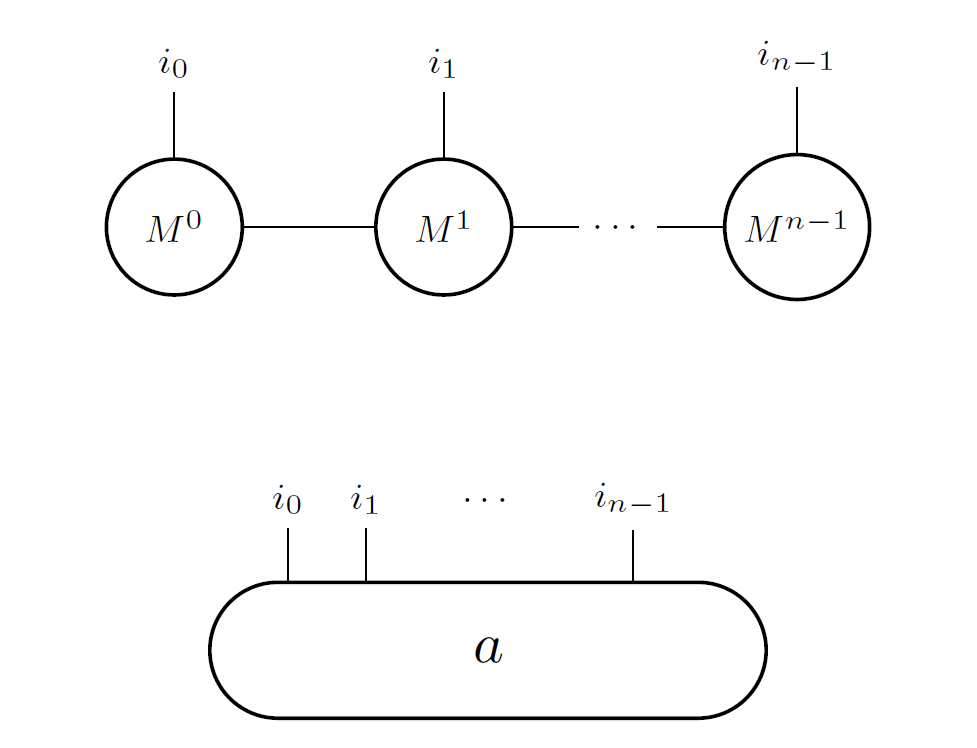
../../../_images/mps_doc_figure.png

Graphical representation of the amplitude tensor, in the linear-algebra simulator (bottom) and in the MPS simulator (top).

Specs and use-cases

Specs:

  • Accepts any gate, up to arity 3.

  • Very efficient simulation of slightly entangling quantum circuits (see use-cases below).

  • Only accepts gates acting on neighbouring qubits. (see lnnize option below, to make any circuit compatible).

Use cases:

  • Can simulate efficiently any circuit that does not produce much entanglement, when starting from \(|0 \dots 0\rangle\). Instances include QFT and arithmetic circuits, which are simulated much faster than with other simulators, and for more qubits, well beyond 50.

  • Can simulate Shor’s algorithm much faster than other simulators (but not with more qubits). This is because at some points during the execution of Shor’s algorithm, entanglement is actually rather low.